La trigonométrie est bien plus qu’une simple branche des mathématiques ; elle joue un rôle fondamental dans notre compréhension des cycles, des ondes et des oscillations. Au cœur de cette science se trouve une relation fascinante entre le cercle trigonométrique et les graphes de fonctions, qui nous permet de visualiser des concepts abstraits de manière concrète. Analyser cette relation peut s’avérer être une aventure riche et palpitante qui nous éclaire sur le comportement des fonctions trigonométriques comme le sinus, le cosinus et la tangente, ainsi que sur leurs propriétés de périodicité, d’amplitude et de phase.

Comprendre le cercle trigonométrique

Le cercle trigonométrique est un outil essentiel en trigonométrie. C’est un cercle de rayon 1, centré à l’origine d’un système d’axes orthogonaux. Chaque point sur le cercle peut être associé à un angle, généralement mesuré en radians, et correspond à des coordonnées cartésiennes qui définissent les valeurs de sinus et cosinus.

Pour mieux saisir ces concepts, voyons les informations clés :

• Rayon : 1, ce qui facilite le calcul.
• Angles : mesurés en radians, où un tour complet correspond à 2π radians.
• Coordonnées : le cosinus de l’angle correspond à l’axe des abscisses et le sinus à l’axe des ordonnées.

Pour illustrer, si nous prenons un angle de π/4 (45 degrés), les coordonnées correspondantes sur le cercle sont (√2/2, √2/2). Ces valeurs représentent à la fois le cosinus et le sinus de cet angle.

Un des aspects intéressants de ce cercle est qu’il permet de visualiser des valeurs sorties d’une infinité de réels x, par exemple, toutes les valeurs de sinus et cosinus d’un angle donné. Cela nous mène à la notion de périodicité, puisque ces valeurs se répètent tous les 2π radians.

Dans cette dynamique, les degrés et les radians sont interconnectés. Par exemple, un angle de 90 degrés correspond à π/2 radians, un angle de 180 degrés à π, et ainsi de suite. Cela nous aide à comprendre le mouvement circulaire et l’oscillation qui suivent les chemins de la trigonométrie.

Les fonctions trigonométriques et leurs propriétés

Les fonctions trigonométriques – sinus, cosinus et tangente – sont des éléments clés qui se manifestent tout au long de notre exploration du cercle trigonométrique. Chacune de ces fonctions a des propriétés spécifiques qui influencent leur apparition sur un graphique.

Les propriétés de ces fonctions incluent :

• Périodicité : Le sinus et le cosinus ont une période de 2π, tandis que la tangente a une période de π.
• Amplitude : Pour le sinus et le cosinus, l’amplitude est de 1, tandis que la tangente n’a pas d’amplitude définie dans ses graphes.
• Phase : La fonction sinus contiendra un décalage vers la droite ou vers la gauche, ce qui influence sa position.

D’étonnantes relations peuvent également être observées entre ces fonctions. Par exemple, on peut exprimer le cosinus d’un angle en fonction du sinus, en utilisant l’identité : cos(x) = sin(π/2 – x). En d’autres termes, le sinus et le cosinus sont intimement liés, comme deux amis qui se complètent l’un l’autre dans une danse harmonieuse.

Graphes de fonctions sinus et cosinus

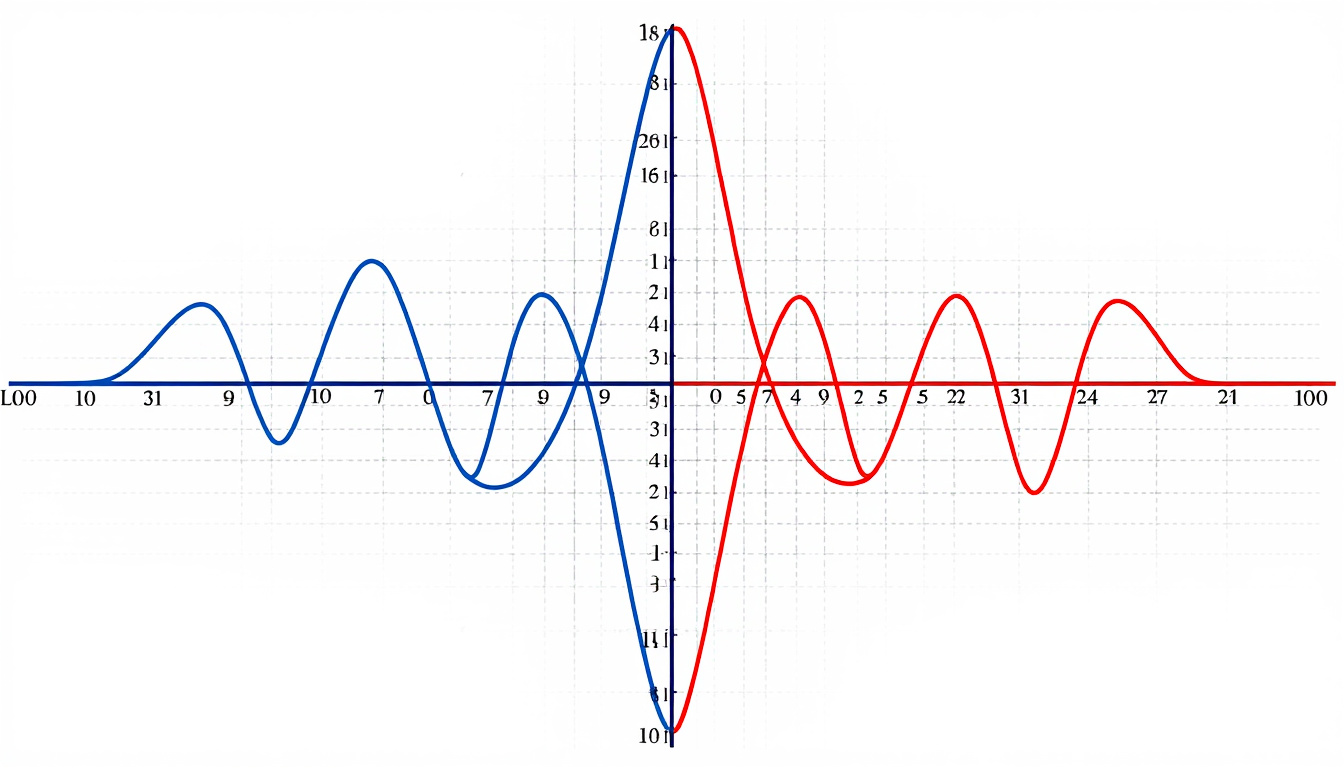
Les graphes de fonctions sinus et cosinus présentent une belle alternance de creux et de sommets, représentant plutôt élégamment leurs valeurs sur les axes. Le graphique du sinus commence à l’origine, tandis que celui du cosinus démarre à son maximum. Ensemble, ils illustrent parfaitement l’oscillation.

Considérons les éléments clés relatifs à ces graphes :

Fonction	Forme du graphique	Départ	Amplitude
Sinus	Ondulant	0	1
Cosinus	Ondulant	1	1
Tangente	Oscillation avec des asymptotes	0	Pas d’amplitude

Ces graphes permettent de visualiser la relation entre l’angle (en radians) et les valeurs de sinus et cosinus. À mesure que l’angle augmente, la fonction sinus monte et descend ; elle atteint des sommets à 1 lorsque l’angle atteint π/2 radians et des creux à -1 lorsque l’angle atteint 3π/2 radians. Cette fluctuation crée une courbe étonnamment prévisible et régulière à observer.

Explorer le graphe de la fonction tangente

La fonction tangente, bien qu’elle soit intrinsèquement liée au sinus et cosinus, présente des comportements à la fois fascinants et surprenants. Son graphique donne l’impression de montagnes russes verticales, car il possède des asymptotes verticales qui se répètent : en effet, tous les π/2 plus un multiple de π représente une indéfinition.

Ces caractéristiques des graphes de tangente sont :

• Période : π.
• Asymptotes : Les points où les valeurs deviennent infinies.
• Entre chacune des asymptotes : le graphique monte de -∞ à +∞.

Pour mieux comprendre cela, examinons un exemple. Prenons une valeur de 0 à π, où la tangente commence à 0, monte à l’infini avant π/2, redescend à l’infini à π et ainsi de suite. Cette continuité suggère une montée progressive qui se convertit en un effondrement dramatique au niveau de ces points d’asymptote, créant un graphique à haute dynamique.

Transformations de fonctions trigonométriques

Les transformations de fonctions sont des outils mathématiques permettant de manipuler graphiquement une fonction. Que ce soit par des translations, des dilatations ou des compressions, ces transformations nous offrent un grand potentiel pour comprendre comment les fonctions trigonométriques interagissent. Cela est particulièrement visible lorsqu’on parle du sinus et du cosinus.

Les transformations peuvent être décomposées en trois types principaux :

• Translation verticale : déplace le graphe vers le haut ou vers le bas.
• Translation horizontale : déplace le graphe vers la droite ou la gauche.
• Dilatation : modifie l’amplitude de la fonction.

Examinons chacun de ces types avec un exemple concret. Supposons que nous avons la fonction de sinus régulière, f(x) = sin(x). Si nous appliquons une translation verticale en ajoutant 2, nous obtenons f(x) = sin(x) + 2, qui va déplacer tout le graphe de sin(x) vers le haut de 2 unités.

Une translation horizontale pourrait impliquer un décalage de 90 degrés à droite : f(x) = sin(x – π/2), ce qui transforme le graphique pour qu’il commence à son maximum.

Applications pratiques de la trigonométrie

La trigonométrie n’est pas qu’une théorie mathématique isolée ; elle a de nombreuses applications pratiques qui influencent nos vies quotidiennes. Des technologies modernes à l’architecture, les concepts trigonométriques sont intégrés à des domaines variés.

Quelques exemples d’applications pratiques incluent :

• Ingénierie et architecture : le calcul des structures et des angles.
• Navigation : en avaiation, pour optimiser les trajectoires de vol.
• Informatiques et graphiques : animation et modélisation de jeux vidéo.

La technologie actuelle utilise des fonctions trigonométriques pour contrôler la dynamique des mouvements. Par exemple, les systèmes de réalité virtuelle s’appuient sur le mouvement angulaire calculé à l’aide de sinus et cosinus pour recréer des environnements immersifs.

Un regard sur les erreurs fréquentes en trigonométrie

Enfin, malgré la beauté et l’élégance de la trigonométrie, plusieurs défis peuvent souvent laisser perplexes les étudiants. Les erreurs les plus fréquentes incluent :

• Confusion entre radians et degrés : Une petite erreur ici peut complètement fausser le résultat !
• Mauvaise interprétation des valeurs négatives : Négliger le fait que les valeurs négatives dans le sinus et le cosinus se situent dans certaines quadrants.
• Oublier les transformations : Ne pas appliquer correctement les transformations aux graphes.

En travaillant avec ces points d’attention, les étudiants peuvent améliorer leur maîtrise de la trigonométrie et renforcer leur compréhension des concepts fondamentaux.

Questions fréquemment posées

Quel est la différence entre sinus et cosinus ? Le sinus est la coordonnée y d’un angle sur le cercle trigonométrique, tandis que le cosinus est la coordonnée x.

Comment se calculent les fonctions trigonométriques pour des angles notables ? Pour les angles notables, vous pouvez mémoriser les valeurs : par exemple, sin(30°) = 1/2, cos(60°) = 1/2.

Qu’est-ce que la tangente d’un angle ? La tangente est le rapport entre le sinus et le cosinus de cet angle (tan(x) = sin(x)/cos(x)).

Pourquoi utilise-t-on le cercle trigonométrique ? Il offre une manière visuelle de comprendre comment les fonctions trigonométriques se comportent à travers des angles différents.

Quelles sont les applications courantes de la trigonométrie ? Les applications incluent l’ingénierie, la navigation, l’animation en jeux vidéo et bien plus encore.